Experiment 12 – Interrupt mechanism

Plot gaps in a waveform to measure the time needed to handle interrupts.

Files

x12-intrmech:
bitbang.c	Generate rapid square wave
startup.c	Startup code
Makefile	Build script
x12.geany	Geany project file

Demonstration

Build and upload the program bitbang.hex. Connect the logic analyser to pins 0, 1 and 2 and capture 10k samples are a rate of 8MHz or so. You will see a rapid square waves on pins 0 and 1. The square wave on pin 0 has occasional pauses that coincide with a pulse on pin 2, but the square wave on pin 1 does not have these pauses.

The file bitbang.c contains a function square_out() that outputs a fast square wave on pin 0, with a period of 16 clock cycles or 1 μs on the V1 micro:bit. The number of nop instructions is carefully chosen to make both the high time and the low time on the pin come to 8 cycles.

    while (1) {
        GPIO.OUTSET = BIT(PAD0);
        nop(); nop(); nop(); nop(); nop(); nop();
        GPIO.OUTCLR = BIT(PAD0);
        nop(); nop(); nop();
    }

The assignment to GPIO.OUTSET has the effect of setting the bit that corresponds to pin 0, and the assignment to GPIO.OUTCLR sets it back to zero again: see below for more explanation of this.

micro:bit version 2

The code provided for V2 has been adjusted to contain many more nop instructions to compensate for the higher clock speed. The function square_out() is marked with the magic word CODERAM: this causes the function to be copied into RAM before the program starts, and removes the unpredictable delays that occur when the micro:bit is executing code from the Flash memory.

The program also configures the chip's hardware random number generator to produce a sequence of random bytes and interrupt whenever a byte is ready. The interrupt handler doesn't do anything with the generated random byte, but just resets the interrupt and produces a brief pulse on pin 2.

/* rng_handler -- interrupt handler for random number generator */
void rng_handler(void)
{
    GPIO.OUTSET = BIT(PAD2);
    RNG.VALRDY = 0;             /* Just acknowledge the interrupt */
    GPIO.OUTCLR = BIT(PAD2);
}

The assignments to GPIO.OUTSET and GPIO.OUTCLR are expanded versions of the calls to gpio_out that would normally be used to set output pins, written here so as to avoid the time overhead of a subroutine call.

By looking at the logic analyser trace, you can see that pulses on pin 2 correspond to hiccups in the square wave produced on pin 1. It's interesting to compare the length of a normal pulse with one of the longer pulses caused by an interrupt. I used an oscilloscope for better resolution, and on a V1 micro:bit measured the width of a longer pulse as 3.56 μs, giving an added time of 3.06 μs, or 49 cycles at 16 MHz. On the V2, the longer pulse had a width of 1.36 μs, giving an added time of 0.86 μs, or 55 cycles at 64 MHz.

A small proportion of this added time comes from actually running the body of the interrupt handler for the random number generator, but most of it comes from looking up the interrupt vector, saving registers on the stack, and restoring them when the interrupt handler returns. You can find more information about interrupt timings on the ARM website.

With a cheap logic analyser, you will not be able to get the same timing resolution as I did with an oscilloscope, but you can at least get figures consistent with mine. You can use the "Timing" protocol decoder (from the same menu as the Serial decoder we used in Experiment 10) to automate the measurement of pulse widths.

Many microcontrollers make it possible to output a high-frequency square wave on a pin without involving the processor in every cycle, so that the signal is undisturbed by interrupts. This is very useful as a way of generating a clock signal for circuits that combine a microcontroller with external digital logic. Sometimes the microcontroller's own clock signal can be routed to a pin, or a timer peripheral can be configured to control an output pin directly.

On the Nordic chips, a similar result can be achieved using the distinctive "Programmable Peripheral Interconnect" (PPI) system, which allows any "event", such as a timer reaching a predefined count, to be connected to a "task", such as toggling a GPIO pin. That is what the bitbang program does on pin 1, by configuring a timer to count at 16 MHz and reset every 8 counts, configuring the "GPIO Tasks and Events" peripheral to provide a task that toggles the pin, and using a channel of the PPI system to connect the task to the timer. See the code for more details. A similar arrangement is used in Experiment 21 to generate the periodic signal that controls a servo-motor.

Activity

The explanation just given for the gaps in the square wave signal seems plausible, but we can probe further by modifying the program and seeing if the modifications have the predicted effect.

1. Make the square wave slower by inserting more nop instructions into the main loop. Do the interruptions continue? Are they as frequent, or do the gaps between interruptions increase also?

2. Make the output signal oscillate faster (but no longer with a perfect square wave) by removing the nop's from the program. What is the shortest width of output pulse that can be produced like this?

3. Try not starting the random number generator by removing or commenting out the line in the main program that says rng_init(). Do the gaps in the square wave output disappear?

4. Remove or comment out the line in rng_init() that says

SET_BIT(RNG_CONFIG, RNG_CONFIG_DERCEN);

This line puts the RNG into a mode where it tries to remove bias towards 0 or 1 in the bits it outputs; when that mode is not enabled, the RNG should produce output more rapidly and more regularly. Do you see the expected effect on the output signal?

5. Try making the interrupt handler run for longer by inserting a delay loop. Do the gaps in the square wave output get longer? What happens if the delay is longer than the typical time between interruptions?

Background

Interrupts behave (from the programmer's point of view) as subroutine calls that are inserted between the instructions of a program, in response to hardware events. So that these subroutine calls do not disrupt the normal functioning of the program, it's important that the entire state of the CPU is preserved by the call. This means not only the data registers, but also the address stored in the link register, and the state of the flags. For example, if a leaf routine is interrupted and has its return address stored in the link register, then that return must be preserved for use when the interrupted routine returns. And if an interrupt comes between the two instructions in a typical compare-and-branch sequence:

cmp r0, r1
beq label

then the flags set by the comparison must be preserved by the interrupt so they can be used to determine whether the branch is taken.

On the Cortex-M0, this is done in such a way that the interrupt handler can be an ordinary subroutine, compiled with the same conventions as any other. That means the compiler that translates each subroutine need not know which ones will be installed as interrupt handlers, and also that no assembly language coding is needed to install and interrupt handler. When an interrupt arrives:

• the processor completes (or, rarely, abandons) the instruction it is executing.
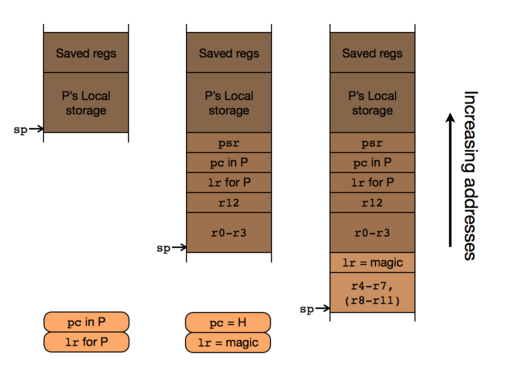
• some of the processor state is saved on the stack. The saved state consists of the program counter, the processor status register (containing the flags), the link register, and registers r0, r1, r2, r3 and r12.
• The link register lr is set to the magic value 0xfffffffd (not a valid address) that will be recognised later.
• The program counter pc is loaded with the address of the interrupt handler. Each device that can interrupt (up to 48 different ones) has a number, and that number is used as an index into a table of interrupt vectors that (on the Nordic chip) is located in ROM at address 0.

The state is now as shown in the middle diagram below, which shows what happens when a subroutine P receives an interrupt with handler H.

Stack states during interrupt entry

A detail: according to ARM conventions, the interrupt handler is entitled to assume that the sp is aligned to a multiple of 8 bytes when it is entered, even though on Cortex-M0 there are no instructions that might depend on this, unlike chips that support double-precision floating point. In order to obey this convention, the machine may pad the saved information with one extra word, record the fact it has done so by setting a special bit in the saved psr value, and compensate appropriately when the interrupt returns. This adjustment is usually invisible to the interrupt handler.

The interrupt handler must obey the normal calling conventions of the machine: if it calls other subroutines (as it may) or uses registers r4-r7 (or, less likely, r8--r11) then it must save lr with its magic value and these registers in its stack frame. So, working together, the hardware and the procedure's prologue save all of r0-r12, plus the pc and lr, and things are arranged so that when the handler returns, it will use the magic value as its return address.

The interrupt handler is now running in a context that is equivalent to the one it would see if it had been called as an ordinary subroutine. It can make free use of registers r0--r3, and can use registers r4--r7 if it has saved them. It can call other subroutines that obey the same calling conventions, and their stack frames will occupy space below its frame and the exception frame on the stack.

When the handler returns, it will restore the values of r4--r11 to the values they had before the interrupt, then branch to the magic value. This signals the processor, instead of loading this value into the pc, to restore the values that were saved by the interrupt mechanism, and the processor returns to the interrupted subroutine. Global variables may have been changed by the interrupt handler – for example, a character may have been received by the UART and put in a buffer – but all the local state is just as it was before the interrupt handler was invoked.

In each program, the table of interrupt handlers is put together by the linker, guided by the linker script device.ld, which specifies they should go at address 0. The code in startup.c makes each vector point to a default handler that flashes the Seven Stars of Death, unless a subroutine with an appropriate name such as uart_handler is defined somewhere in the program.

In the Cortex-M0, the management of interrupts is delegated to a semi-detached functional unit called the Nested Vectored Interrupt Controller (NVIC). We need to know about this, because to use interrupts, three separate units must be set up properly: the device, so that it requests an interrupt when certain events happen; the NVIC, so that it enables and gives an appropriate priority to interrupts from the device, and the CPU itself, so that it responds to interrupt requests. The name of the NVIC gives a clue to some aspects of its operation:

• It supports nested interrupts – that is, each device is given a configurable priority, and during the handling of an interrupt from a low-priority device, interrupts from higher-priority devices may happen. We will not use this, but will soon move to an operating system where most interrupt handlers are very short and just convert the interrupt into a message: this removes the worry that handling one interrupt will block another one for too long. Note that, in any case, a device cannot have higher priority than itself, so the interrupt handler for a device completes before another interrupt from the device is accepted.
• This (delaying interrupts until the CPU is ready for them) works because the NVIC keeps track of which devices have pending interrupts, and will send requests to the CPU when it can handle them. There is just one pending interrupt for each device, so if we want (for example) to count interrupts as clock ticks, then we must be sure to service each interrupt before the next one arrives.
• Interrupts are vectored – that is, each device can have a separate interrupt handler, rather than (say) having one handler for all interrupts that must then work out which device(s) sent the request. Note, however, that a device can generate interrupts for multiple reasons, so the handler must then work out why the interrupt happened, and respond appropriately. For example, the UART can interrupt when it is ready to output a fresh character, but also when it has received a character that it is ready to pass the the CPU.

Interrupts can be disabled in several ways: all interrupts can be disabled and enabled in the CPU by using the functions intr_disable() and intr_enable() that are aliases for the instructions cpsie i and cpsid i. We can also disable interrupts from a specific device by using the functions disable_irq(irq) and enable_irq(irq). Interrupts for specific events can also be enabled and disabled by using the device registers for a specific device.

There are a couple of system-level interrupts (also called exceptions) that are not associated with any particular device. One of these is the HardFault exception that is triggered when a program attempts an undefined action, such as an unaligned load or store. In our software, the handler for the HardFault exception shows the seven stars of death. That's appropriate for a program running in am experiment, because it lets us see immediately that something has gone wrong. If the program is part of an embedded device, it's necessary to be much careful about what happens when a fault is detected, whether it is caused by malfunctioning hardware or by a programming mistake. The proper thing to do might be to bring everything to a safe stop, making as few assumptions as possible about the state of the device.

Another kind of system event is triggered when the processor executes an svc (supervisor call) instruction. When we introduce an operating system, this will mean that there is a uniform way of entering the operating system, whether it is entered because of a hardware event or a software request. On machines (the Nordic chip isn't one of them) where application programs run with less privileges than the operating system, the svc instruction is also the means for crossing the boundary between unprivileged and privileged programs.

Context

The interrupt mechanism of the Cortex-M0 is unusual in obeying its own calling conventions: that is to say, the actions on interrupt call and return exactly match the conventions assumed by compilers for the machine. This makes it possible for interrupt handlers to be subroutines written in a high-level language and compiled in the ordinary way. It's more normal for machines to save only a minimal amount of state when an interrupt happens: perhaps just the program counter and processor status word are pushed on a stack, and the program counter is loaded with the handler address. When the interrupt handler wants to return, it must use a special instruction rti that restores the program counter and status word from the stack, rather than the usual instruction for returning from a subroutine. If we want to write interrupt handlers in a high-level language, then a little adapter written in assembly language is needed. It saves the rest of the state including the register contents (or at least those registers that are not preserved according to the calling convention), then calls the subroutine; and when the subroutine returns, it uses an rti instruction to return from the interrupt. Of course, it is possible for the machine-language shim that saves and restores the processor state to be generated by a compiler, and on some machines the compiler lets you mark a C function specially, so that it becomes an interrupt handler rather than an ordinary function. The simpler kind of interrupt mechanism has some advantages: simpler hardware, for one, and the possibility of hand-crafting an interrupt handler in assembly language that runs more quickly by saving and restoring only part of the state.

Microcontrollers often make it possible to output a signal from one of the in-built counter/timers on an I/O pin in order to provide an external square wave at high frequency that is not disturbed by interrupts, and does not occupy the CPU. Some microcontrollers make this a specific feature of their counter/timers, but on the nRF51822 it can be achieved by using the Programmed Peripheral Interconnect (PPI) module to link a timer with a GPIO task. The source file bitbang.c contains a subroutine sqwave_init that enables an 8MHz square wave (half the system clock frequency) on pin 0. It configures Timer 2 to count at 16 MHz, resetting on every clock pulse, and a PPI channel is configured to link the event of the timer resetting to a GPIO task that toggles the pin. You can enable this signal by uncommenting the call to sqwave_init in the main program. An 8MHz square wave is beyond the frequency that can be accurately captured by a logic analyser sampling at 24M samples/second, but you can view the signal better either by connecting an oscilloscope with a higher sample rate, or by reducing the frequency by editing the timer setup, increasing the value used to set TIMER2.CC[0]. You will be able to see that interrupts do not affect the signal at all.

Challenges

The demonstration program contains a very minimal driver for the random number generator. Enhance it to make a driver that gives proper access to the stream of random numbers, perhaps storing random bytes in a buffer as they are generated, and providing subroutines that deliver a random byte or a random integer. The hardware is documented in Chapter 21 of the nRF51 Series Reference Manual, and appropriate constant addresses are defined in hardware.h.

Use your implementation first in an application that prints a sequence of random numbers in a specified range (such as random dice rolls). Make another application that generates and prints a histogram of random values like this:

1: **********************
2: ***************************
3: ********************
4: ***********************
5: *****************************
6: ******************

Are the results consistent with a truly random source?

Questions

How does the RNG's bias elimination algorithm work?

The method is due to John von Neumann, and can be explained by thinking about a biassed coin, equivalent to a biassed process that produces a 0 or 1 bit by sampling electrical noise. To produce an unbiassed Head or Tail, toss the coin twice: if the two tosses are different, take the first toss as the result, so that HT produces H and TH produces T. If the two tosses are the same, then begin again from the start, perhaps using several pairs of tosses before getting two tosses that are different.

If tosses are independent and produce Heads with probability p and Tails with probability q = 1 − p, then the results of two tosses are HH with probability p², HT or TH both with probability pq, and TT with probability q². Thus HT and TH are equally likely, and the experiment must be repeated with probability 1 − 2pq. The number of trials needed has a geometric distribution with mean 1/(1 − 2pq), smallest if p = q = 1/2, when the mean is 2. As the coin becomes more biassed, the mean number of trials grows, but the results remain unbiassed.

To generate a random dice roll given a source of random bytes in the range 0 up to 255, you can take a byte and divide it by 42, truncating the result to an integer. If the answer is between 0 and 5 inclusive, then add 1 to give the dice roll. If the byte was 252, 253, 254 or 255, then the division will produce 6 as the result, and you should try again.